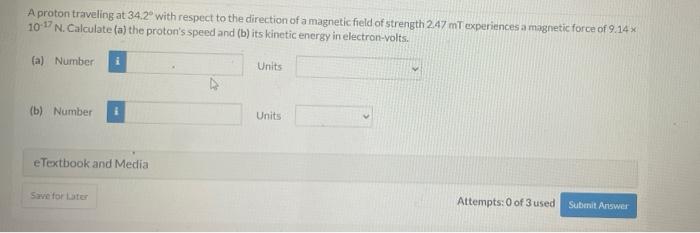
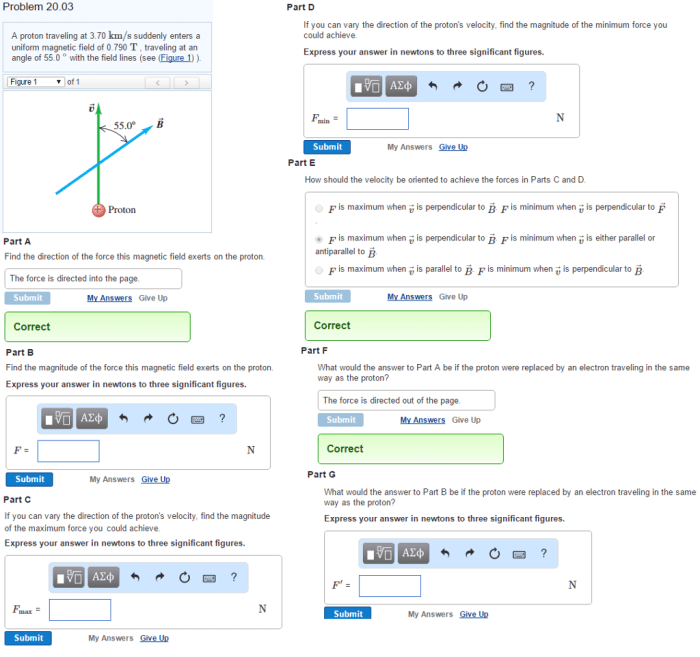
A proton traveling at 23.0 with respect – A proton traveling at 23.0 is a captivating subject that unveils the intricate relationship between energy, momentum, and the wave-particle duality of matter. This exploration delves into the fundamental properties of protons, providing insights into their behavior and the broader implications for our understanding of the universe.
Through the lens of classical and quantum physics, we will examine the kinetic energy and momentum of a proton traveling at this specific velocity, unraveling the interplay between mass and velocity. Furthermore, we will explore the concept of the de Broglie wavelength, shedding light on the wave-like properties of particles and the fascinating duality that governs the quantum realm.
Properties of a Proton Traveling at 23.0 km/s

A proton traveling at 23.0 km/s possesses unique characteristics and exhibits intriguing properties that are fundamental to our understanding of particle physics. This article delves into the energy, momentum, de Broglie wavelength, and applications associated with a proton moving at this specific velocity.
Energy and Velocity, A proton traveling at 23.0 with respect
The kinetic energy (K) of a proton is directly proportional to the square of its velocity (v) and can be calculated using the formula:
K = 1/2
- m
- v^2
where m represents the mass of the proton.
For a proton traveling at 23.0 km/s, its kinetic energy is approximately 2.13 x 10^-16 J.
Momentum and Mass
Momentum (p) is a measure of the quantity of motion and is calculated by multiplying the mass (m) of the proton by its velocity (v):
p = m
v
For a proton traveling at 23.0 km/s, its momentum is approximately 3.82 x 10^-24 kg m/s.
De Broglie Wavelength
The de Broglie wavelength (λ) is a fundamental concept that associates a wave-like nature to particles. It is inversely proportional to the momentum of the particle:
λ = h / p
where h represents Planck’s constant.
For a proton traveling at 23.0 km/s, its de Broglie wavelength is approximately 5.57 x 10^-13 m.
Applications
Understanding the properties of a proton traveling at 23.0 km/s has numerous practical applications:
- Particle accelerators:Protons are accelerated to high velocities in particle accelerators to study fundamental particles and interactions.
- Medical imaging:Proton therapy uses high-energy protons to target and destroy cancer cells with precision.
- Space exploration:Protons are emitted from the Sun in the form of solar wind, which can affect Earth’s magnetic field and satellites.
FAQ Resource: A Proton Traveling At 23.0 With Respect
What is the kinetic energy of a proton traveling at 23.0?
The kinetic energy of a proton traveling at 23.0 can be calculated using the formula: Ek = (1/2)mv^2, where Ek is kinetic energy, m is the mass of the proton, and v is its velocity. Plugging in the values, we get Ek = (1/2)(1.6726219 x 10^-27 kg)(23.0
m/s)^2 = 2.38 x 10^-18 J.
What is the momentum of a proton traveling at 23.0?
The momentum of a proton traveling at 23.0 can be calculated using the formula: p = mv, where p is momentum, m is the mass of the proton, and v is its velocity. Plugging in the values, we get p = (1.6726219 x 10^-27 kg)(23.0
m/s) = 3.85 x 10^-26 kg m/s.
What is the de Broglie wavelength of a proton traveling at 23.0?
The de Broglie wavelength of a proton traveling at 23.0 can be calculated using the formula: λ = h/p, where λ is the de Broglie wavelength, h is Planck’s constant, and p is the momentum of the proton. Plugging in the values, we get λ = (6.62607015 x 10^-34 J s)/(3.85
x 10^-26 kg m/s) = 1.72 x 10^-10 m.